FreeStatistics.org

Free Statistics

of Irreproducible Research!

Description of Statistical Computation

Author's title

Author*The author of this computation has been verified*
R Software Modulerwasp_arimabackwardselection.wasp
Title produced by softwareARIMA Backward Selection
Date of computationFri, 16 Dec 2016 14:36:55 +0100
Cite this page as followsStatistical Computations at FreeStatistics.org, Office for Research Development and Education, URL https://freestatistics.org/blog/index.php?v=date/2016/Dec/16/t1481895455f1h5m5g63vuk94z.htm/, Retrieved Fri, 01 Nov 2024 03:40:38 +0000
Statistical Computations at FreeStatistics.org, Office for Research Development and Education, URL https://freestatistics.org/blog/index.php?pk=300258, Retrieved Fri, 01 Nov 2024 03:40:38 +0000
QR Codes:

Original text written by user:
IsPrivate?No (this computation is public)
User-defined keywords
Estimated Impact124

Tree of Dependent Computations

Family? (F = Feedback message, R = changed R code, M = changed R Module, P = changed Parameters, D = changed Data)
-       [ARIMA Backward Selection] [] [2016-12-16 13:36:55] [404ac5ee4f7301873f6a96ef36861981] [Current]
- RM      [ARIMA Forecasting] [] [2016-12-16 13:40:22] [683f400e1b95307fc738e729f07c4fce]
- RM      [Exponential Smoothing] [] [2016-12-16 13:42:25] [683f400e1b95307fc738e729f07c4fce]
- RMP       [ARIMA Backward Selection] [] [2016-12-18 21:37:02] [683f400e1b95307fc738e729f07c4fce]
- RMP       [ARIMA Backward Selection] [] [2016-12-18 22:30:58] [683f400e1b95307fc738e729f07c4fce]
- RM          [ARIMA Forecasting] [] [2016-12-18 22:55:26] [683f400e1b95307fc738e729f07c4fce]
- R P           [ARIMA Forecasting] [] [2016-12-19 19:52:13] [683f400e1b95307fc738e729f07c4fce]
- RM D    [Univariate Data Series] [] [2016-12-16 13:46:10] [683f400e1b95307fc738e729f07c4fce]
- RM D    [Univariate Data Series] [] [2016-12-16 14:00:03] [683f400e1b95307fc738e729f07c4fce]
- RM D    [(Partial) Autocorrelation Function] [] [2016-12-16 14:01:20] [683f400e1b95307fc738e729f07c4fce]
- RM D    [Variance Reduction Matrix] [] [2016-12-16 14:05:33] [683f400e1b95307fc738e729f07c4fce]
- RM D    [Exponential Smoothing] [] [2016-12-16 14:08:14] [683f400e1b95307fc738e729f07c4fce]
- RM D    [Univariate Data Series] [] [2016-12-16 14:11:09] [683f400e1b95307fc738e729f07c4fce]
- RM D    [(Partial) Autocorrelation Function] [] [2016-12-16 14:12:27] [683f400e1b95307fc738e729f07c4fce]
- RM D    [Spectral Analysis] [] [2016-12-16 14:14:12] [683f400e1b95307fc738e729f07c4fce]
- RM D    [Variance Reduction Matrix] [] [2016-12-16 14:15:08] [683f400e1b95307fc738e729f07c4fce]
-    D    [ARIMA Backward Selection] [] [2016-12-16 14:17:56] [683f400e1b95307fc738e729f07c4fce]
- RM        [ARIMA Forecasting] [] [2016-12-16 14:21:10] [683f400e1b95307fc738e729f07c4fce]
- RM        [Exponential Smoothing] [] [2016-12-16 14:22:17] [683f400e1b95307fc738e729f07c4fce]
- RM D      [Univariate Data Series] [] [2016-12-16 14:24:18] [683f400e1b95307fc738e729f07c4fce]
- RM D      [(Partial) Autocorrelation Function] [] [2016-12-16 14:26:32] [683f400e1b95307fc738e729f07c4fce]
- RM D      [Variance Reduction Matrix] [] [2016-12-16 14:27:44] [683f400e1b95307fc738e729f07c4fce]
- RM D      [Spectral Analysis] [] [2016-12-16 14:28:53] [683f400e1b95307fc738e729f07c4fce]
- RM D      [Exponential Smoothing] [] [2016-12-16 14:33:21] [683f400e1b95307fc738e729f07c4fce]
- RM D      [Structural Time Series Models] [] [2016-12-16 14:34:17] [683f400e1b95307fc738e729f07c4fce]
- RM D      [Univariate Data Series] [] [2016-12-16 14:36:27] [683f400e1b95307fc738e729f07c4fce]
- RM D      [Variance Reduction Matrix] [] [2016-12-16 14:39:33] [683f400e1b95307fc738e729f07c4fce]
- RM D      [Spectral Analysis] [] [2016-12-16 14:42:19] [683f400e1b95307fc738e729f07c4fce]
- RM D      [(Partial) Autocorrelation Function] [] [2016-12-16 14:44:35] [683f400e1b95307fc738e729f07c4fce]
- RM D      [Exponential Smoothing] [] [2016-12-16 14:47:58] [683f400e1b95307fc738e729f07c4fce]
- R  D      [ARIMA Backward Selection] [] [2016-12-16 14:51:40] [683f400e1b95307fc738e729f07c4fce]
- RM          [ARIMA Forecasting] [] [2016-12-16 14:54:52] [683f400e1b95307fc738e729f07c4fce]
- RM D        [Univariate Data Series] [] [2016-12-16 15:07:18] [683f400e1b95307fc738e729f07c4fce]
- RM D        [(Partial) Autocorrelation Function] [] [2016-12-16 15:11:19] [683f400e1b95307fc738e729f07c4fce]
- RM D        [Variance Reduction Matrix] [] [2016-12-16 15:12:05] [683f400e1b95307fc738e729f07c4fce]
- RM D        [Spectral Analysis] [] [2016-12-16 15:14:16] [683f400e1b95307fc738e729f07c4fce]
- R  D        [ARIMA Backward Selection] [] [2016-12-16 15:17:08] [683f400e1b95307fc738e729f07c4fce]
- RM D        [Exponential Smoothing] [] [2016-12-16 15:22:42] [683f400e1b95307fc738e729f07c4fce]
- RM D        [Univariate Data Series] [] [2016-12-16 15:24:03] [683f400e1b95307fc738e729f07c4fce]
- RM D        [(Partial) Autocorrelation Function] [] [2016-12-16 15:30:48] [683f400e1b95307fc738e729f07c4fce]
- RM D        [Spectral Analysis] [] [2016-12-16 15:34:39] [683f400e1b95307fc738e729f07c4fce]
- RM D        [Variance Reduction Matrix] [] [2016-12-16 15:35:21] [683f400e1b95307fc738e729f07c4fce]
- RM D        [(Partial) Autocorrelation Function] [] [2016-12-16 15:37:16] [683f400e1b95307fc738e729f07c4fce]
- RM D        [Classical Decomposition] [] [2016-12-16 15:38:17] [683f400e1b95307fc738e729f07c4fce]
- RM D        [Decomposition by Loess] [] [2016-12-16 15:40:09] [683f400e1b95307fc738e729f07c4fce]
- RM D        [Structural Time Series Models] [] [2016-12-16 15:41:08] [683f400e1b95307fc738e729f07c4fce]
- RM D        [Exponential Smoothing] [] [2016-12-16 15:42:09] [683f400e1b95307fc738e729f07c4fce]
- R  D        [ARIMA Backward Selection] [] [2016-12-16 15:45:16] [683f400e1b95307fc738e729f07c4fce]
- RM D        [ARIMA Forecasting] [] [2016-12-16 15:46:48] [683f400e1b95307fc738e729f07c4fce]

[Truncated]
Feedback Forum

Post a new message

Dataset

Dataseries X:
Download CSV
Histogram
Boxplots 
6086
6090.5
6103.5
6144
6190.5
6225
6272
6294
6366
6426
6477
6500
6538
6581
6615.5
6639.5
6651
6665
6684
6684.5
6666.5
6666.5
6651
6652
6647
6618.5
6604.5
6572
6556
6535
6515.5
6515
6489
6491
6483.5
6486.5
6486.5
6478.5
6461
6458.5
6446
6420
6397.5
6408
6408.5
6401.5
6408.5
6417.5
6406.5
6426.5
6431.5
6441.5
6446
6450
6468
6488.5
6512
6525
6551
6567.5
6560.5
6572
6574.5
6583.5
6589.5
6600
6601
6586
6590
6616
6641.5
6647
6662
6663.5
6663
6653.5
6642.5
6624.5
6605.5
6604.5
6575
6566
6562.5
6560.5
6502
6552.5
6542.5
6536
6516.5
6506.5
6491.5
6469.5
6445
6426
6355.5
6340
6307.5
6254.5
6230.5
6213
6212.5
6203
6204
6220.5
6205
6199.5
6184.5
6169
6140.5
6144.5
6145.5
6148.5
6145
6133
6138
6104.5
6090.5

Tables (Output of Computation)





Summary of computational transaction
Raw Input view raw input (R code)
Raw Outputview raw output of R engine
Computing time3 seconds
R ServerBig Analytics Cloud Computing Center

\begin{tabular}{lllllllll}
\hline
Summary of computational transaction \tabularnewline
Raw Input view raw input (R code)  \tabularnewline
Raw Outputview raw output of R engine  \tabularnewline
Computing time3 seconds \tabularnewline
R ServerBig Analytics Cloud Computing Center \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=300258&T=0

[TABLE]
[ROW]
Summary of computational transaction[/C][/ROW] [ROW]Raw Input[/C] view raw input (R code) [/C][/ROW] [ROW]Raw Output[/C]view raw output of R engine [/C][/ROW] [ROW]Computing time[/C]3 seconds[/C][/ROW] [ROW]R Server[/C]Big Analytics Cloud Computing Center[/C][/ROW] [/TABLE] Source: https://freestatistics.org/blog/index.php?pk=300258&T=0

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=300258&T=0

As an alternative you can also use a QR Code:  
QR Code


The GUIDs for individual cells are displayed in the table below:

Summary of computational transaction
Raw Input view raw input (R code)
Raw Outputview raw output of R engine
Computing time3 seconds
R ServerBig Analytics Cloud Computing Center






ARIMA Parameter Estimation and Backward Selection
Iterationar1ar2ar3ma1sar1
Estimates ( 1 )-0.8603-0.5199-0.2357-0.3480.4598
(p-val)(5e-04 )(0.0373 )(0.1001 )(0.6397 )(0.4468 )
Estimates ( 2 )-0.9165-0.5439-0.235500.1673
(p-val)(0.0031 )(0.0756 )(0.1368 )(NA )(0.5914 )
Estimates ( 3 )-0.7562-0.4074-0.175400
(p-val)(0 )(5e-04 )(0.0661 )(NA )(NA )
Estimates ( 4 )-0.705-0.2793000
(p-val)(0 )(0.0028 )(NA )(NA )(NA )
Estimates ( 5 )NANANANANA
(p-val)(NA )(NA )(NA )(NA )(NA )
Estimates ( 6 )NANANANANA
(p-val)(NA )(NA )(NA )(NA )(NA )
Estimates ( 7 )NANANANANA
(p-val)(NA )(NA )(NA )(NA )(NA )
Estimates ( 8 )NANANANANA
(p-val)(NA )(NA )(NA )(NA )(NA )
Estimates ( 9 )NANANANANA
(p-val)(NA )(NA )(NA )(NA )(NA )

\begin{tabular}{lllllllll}
\hline
ARIMA Parameter Estimation and Backward Selection \tabularnewline
Iteration & ar1 & ar2 & ar3 & ma1 & sar1 \tabularnewline
Estimates ( 1 ) & -0.8603 & -0.5199 & -0.2357 & -0.348 & 0.4598 \tabularnewline
(p-val) & (5e-04 ) & (0.0373 ) & (0.1001 ) & (0.6397 ) & (0.4468 ) \tabularnewline
Estimates ( 2 ) & -0.9165 & -0.5439 & -0.2355 & 0 & 0.1673 \tabularnewline
(p-val) & (0.0031 ) & (0.0756 ) & (0.1368 ) & (NA ) & (0.5914 ) \tabularnewline
Estimates ( 3 ) & -0.7562 & -0.4074 & -0.1754 & 0 & 0 \tabularnewline
(p-val) & (0 ) & (5e-04 ) & (0.0661 ) & (NA ) & (NA ) \tabularnewline
Estimates ( 4 ) & -0.705 & -0.2793 & 0 & 0 & 0 \tabularnewline
(p-val) & (0 ) & (0.0028 ) & (NA ) & (NA ) & (NA ) \tabularnewline
Estimates ( 5 ) & NA & NA & NA & NA & NA \tabularnewline
(p-val) & (NA ) & (NA ) & (NA ) & (NA ) & (NA ) \tabularnewline
Estimates ( 6 ) & NA & NA & NA & NA & NA \tabularnewline
(p-val) & (NA ) & (NA ) & (NA ) & (NA ) & (NA ) \tabularnewline
Estimates ( 7 ) & NA & NA & NA & NA & NA \tabularnewline
(p-val) & (NA ) & (NA ) & (NA ) & (NA ) & (NA ) \tabularnewline
Estimates ( 8 ) & NA & NA & NA & NA & NA \tabularnewline
(p-val) & (NA ) & (NA ) & (NA ) & (NA ) & (NA ) \tabularnewline
Estimates ( 9 ) & NA & NA & NA & NA & NA \tabularnewline
(p-val) & (NA ) & (NA ) & (NA ) & (NA ) & (NA ) \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=300258&T=1

[TABLE]
[ROW][C]ARIMA Parameter Estimation and Backward Selection[/C][/ROW]
[ROW][C]Iteration[/C][C]ar1[/C][C]ar2[/C][C]ar3[/C][C]ma1[/C][C]sar1[/C][/ROW]
[ROW][C]Estimates ( 1 )[/C][C]-0.8603[/C][C]-0.5199[/C][C]-0.2357[/C][C]-0.348[/C][C]0.4598[/C][/ROW]
[ROW][C](p-val)[/C][C](5e-04 )[/C][C](0.0373 )[/C][C](0.1001 )[/C][C](0.6397 )[/C][C](0.4468 )[/C][/ROW]
[ROW][C]Estimates ( 2 )[/C][C]-0.9165[/C][C]-0.5439[/C][C]-0.2355[/C][C]0[/C][C]0.1673[/C][/ROW]
[ROW][C](p-val)[/C][C](0.0031 )[/C][C](0.0756 )[/C][C](0.1368 )[/C][C](NA )[/C][C](0.5914 )[/C][/ROW]
[ROW][C]Estimates ( 3 )[/C][C]-0.7562[/C][C]-0.4074[/C][C]-0.1754[/C][C]0[/C][C]0[/C][/ROW]
[ROW][C](p-val)[/C][C](0 )[/C][C](5e-04 )[/C][C](0.0661 )[/C][C](NA )[/C][C](NA )[/C][/ROW]
[ROW][C]Estimates ( 4 )[/C][C]-0.705[/C][C]-0.2793[/C][C]0[/C][C]0[/C][C]0[/C][/ROW]
[ROW][C](p-val)[/C][C](0 )[/C][C](0.0028 )[/C][C](NA )[/C][C](NA )[/C][C](NA )[/C][/ROW]
[ROW][C]Estimates ( 5 )[/C][C]NA[/C][C]NA[/C][C]NA[/C][C]NA[/C][C]NA[/C][/ROW]
[ROW][C](p-val)[/C][C](NA )[/C][C](NA )[/C][C](NA )[/C][C](NA )[/C][C](NA )[/C][/ROW]
[ROW][C]Estimates ( 6 )[/C][C]NA[/C][C]NA[/C][C]NA[/C][C]NA[/C][C]NA[/C][/ROW]
[ROW][C](p-val)[/C][C](NA )[/C][C](NA )[/C][C](NA )[/C][C](NA )[/C][C](NA )[/C][/ROW]
[ROW][C]Estimates ( 7 )[/C][C]NA[/C][C]NA[/C][C]NA[/C][C]NA[/C][C]NA[/C][/ROW]
[ROW][C](p-val)[/C][C](NA )[/C][C](NA )[/C][C](NA )[/C][C](NA )[/C][C](NA )[/C][/ROW]
[ROW][C]Estimates ( 8 )[/C][C]NA[/C][C]NA[/C][C]NA[/C][C]NA[/C][C]NA[/C][/ROW]
[ROW][C](p-val)[/C][C](NA )[/C][C](NA )[/C][C](NA )[/C][C](NA )[/C][C](NA )[/C][/ROW]
[ROW][C]Estimates ( 9 )[/C][C]NA[/C][C]NA[/C][C]NA[/C][C]NA[/C][C]NA[/C][/ROW]
[ROW][C](p-val)[/C][C](NA )[/C][C](NA )[/C][C](NA )[/C][C](NA )[/C][C](NA )[/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=300258&T=1

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=300258&T=1

As an alternative you can also use a QR Code:  
QR Code


The GUIDs for individual cells are displayed in the table below:

ARIMA Parameter Estimation and Backward Selection
Iterationar1ar2ar3ma1sar1
Estimates ( 1 )-0.8603-0.5199-0.2357-0.3480.4598
(p-val)(5e-04 )(0.0373 )(0.1001 )(0.6397 )(0.4468 )
Estimates ( 2 )-0.9165-0.5439-0.235500.1673
(p-val)(0.0031 )(0.0756 )(0.1368 )(NA )(0.5914 )
Estimates ( 3 )-0.7562-0.4074-0.175400
(p-val)(0 )(5e-04 )(0.0661 )(NA )(NA )
Estimates ( 4 )-0.705-0.2793000
(p-val)(0 )(0.0028 )(NA )(NA )(NA )
Estimates ( 5 )NANANANANA
(p-val)(NA )(NA )(NA )(NA )(NA )
Estimates ( 6 )NANANANANA
(p-val)(NA )(NA )(NA )(NA )(NA )
Estimates ( 7 )NANANANANA
(p-val)(NA )(NA )(NA )(NA )(NA )
Estimates ( 8 )NANANANANA
(p-val)(NA )(NA )(NA )(NA )(NA )
Estimates ( 9 )NANANANANA
(p-val)(NA )(NA )(NA )(NA )(NA )






Estimated ARIMA Residuals
Value
-8.15513924605754
6.6880747370819
30.3742897379884
27.4024834450249
5.23270647013269
10.6950658059182
-19.3845551204331
34.083585584327
17.8153344133407
-2.08801002514429
-30.9230274545953
-11.9448080706406
3.35535603803601
-3.5197735358106
-12.2587168154232
-23.0257914520334
-12.7213614723632
-0.0446052607539968
-15.8935035121303
-30.0133113035481
-2.64949333691038
-12.6721192504347
8.86774823327596
3.31929351204326
-24.0335217807969
-2.81987022216345
-18.1629581890056
4.29604777202076
2.48296269181537
1.19634190483794
20.9917311367481
-11.3988511275893
16.7222053313835
4.61627418154512
10.2510768830507
5.98125858041203
-7.65703782555465
-14.9295832775051
4.03061921084373
-3.93162652161573
-16.616737696635
-8.15110360171093
28.3918415384869
14.0111632814351
-1.00222715300333
10.0437132119523
7.77621215996896
-14.0993071013754
19.1476224685539
0.643293957320566
2.77936012261853
-2.39225779963363
-5.25324600008298
12.2581851008354
11.9177249840377
10.5068162677944
-4.75682779044291
6.72114746146599
-3.42161933345778
-27.2289625585208
-0.859919505719517
-6.25231192010506
3.10937796290273
1.49368491101177
3.30093161643163
-6.17923825024445
-21.8764192059589
3.82013829760581
28.1815483184555
21.0700175513575
-8.08121925508476
-1.96749547034415
-14.5528731974646
-11.8462839345448
-14.3461058408639
-11.4887360613639
-12.1520508002723
-8.48323010597232
14.1286234902946
-16.5244786159565
6.10768292981265
12.5472797746834
9.01149570083362
-49.5284439444977
67.8526324077829
-0.834877985582352
-7.74949071339142
-15.8810126454209
-9.51791124314787
-2.4990775220067
-9.19082794705264
-8.16372485074317
-0.119646415903844
-49.5877162220649
17.8597386231158
4.57104866289501
-19.9806671545839
16.2210437593785
17.0939906922749
30.1343505324357
11.5907664565084
11.7612514894472
22.7551997743467
-17.580238997075
-6.03999798933819
-12.2570842732057
-9.22311072866705
-15.4943911196951
20.7994902083319
16.1910165667978
10.6925545206068
-0.508362965810193
-13.1265117907278
8.27511266420879
-30.2487049945539
-4.17717699887999

\begin{tabular}{lllllllll}
\hline
Estimated ARIMA Residuals \tabularnewline
Value \tabularnewline
-8.15513924605754 \tabularnewline
6.6880747370819 \tabularnewline
30.3742897379884 \tabularnewline
27.4024834450249 \tabularnewline
5.23270647013269 \tabularnewline
10.6950658059182 \tabularnewline
-19.3845551204331 \tabularnewline
34.083585584327 \tabularnewline
17.8153344133407 \tabularnewline
-2.08801002514429 \tabularnewline
-30.9230274545953 \tabularnewline
-11.9448080706406 \tabularnewline
3.35535603803601 \tabularnewline
-3.5197735358106 \tabularnewline
-12.2587168154232 \tabularnewline
-23.0257914520334 \tabularnewline
-12.7213614723632 \tabularnewline
-0.0446052607539968 \tabularnewline
-15.8935035121303 \tabularnewline
-30.0133113035481 \tabularnewline
-2.64949333691038 \tabularnewline
-12.6721192504347 \tabularnewline
8.86774823327596 \tabularnewline
3.31929351204326 \tabularnewline
-24.0335217807969 \tabularnewline
-2.81987022216345 \tabularnewline
-18.1629581890056 \tabularnewline
4.29604777202076 \tabularnewline
2.48296269181537 \tabularnewline
1.19634190483794 \tabularnewline
20.9917311367481 \tabularnewline
-11.3988511275893 \tabularnewline
16.7222053313835 \tabularnewline
4.61627418154512 \tabularnewline
10.2510768830507 \tabularnewline
5.98125858041203 \tabularnewline
-7.65703782555465 \tabularnewline
-14.9295832775051 \tabularnewline
4.03061921084373 \tabularnewline
-3.93162652161573 \tabularnewline
-16.616737696635 \tabularnewline
-8.15110360171093 \tabularnewline
28.3918415384869 \tabularnewline
14.0111632814351 \tabularnewline
-1.00222715300333 \tabularnewline
10.0437132119523 \tabularnewline
7.77621215996896 \tabularnewline
-14.0993071013754 \tabularnewline
19.1476224685539 \tabularnewline
0.643293957320566 \tabularnewline
2.77936012261853 \tabularnewline
-2.39225779963363 \tabularnewline
-5.25324600008298 \tabularnewline
12.2581851008354 \tabularnewline
11.9177249840377 \tabularnewline
10.5068162677944 \tabularnewline
-4.75682779044291 \tabularnewline
6.72114746146599 \tabularnewline
-3.42161933345778 \tabularnewline
-27.2289625585208 \tabularnewline
-0.859919505719517 \tabularnewline
-6.25231192010506 \tabularnewline
3.10937796290273 \tabularnewline
1.49368491101177 \tabularnewline
3.30093161643163 \tabularnewline
-6.17923825024445 \tabularnewline
-21.8764192059589 \tabularnewline
3.82013829760581 \tabularnewline
28.1815483184555 \tabularnewline
21.0700175513575 \tabularnewline
-8.08121925508476 \tabularnewline
-1.96749547034415 \tabularnewline
-14.5528731974646 \tabularnewline
-11.8462839345448 \tabularnewline
-14.3461058408639 \tabularnewline
-11.4887360613639 \tabularnewline
-12.1520508002723 \tabularnewline
-8.48323010597232 \tabularnewline
14.1286234902946 \tabularnewline
-16.5244786159565 \tabularnewline
6.10768292981265 \tabularnewline
12.5472797746834 \tabularnewline
9.01149570083362 \tabularnewline
-49.5284439444977 \tabularnewline
67.8526324077829 \tabularnewline
-0.834877985582352 \tabularnewline
-7.74949071339142 \tabularnewline
-15.8810126454209 \tabularnewline
-9.51791124314787 \tabularnewline
-2.4990775220067 \tabularnewline
-9.19082794705264 \tabularnewline
-8.16372485074317 \tabularnewline
-0.119646415903844 \tabularnewline
-49.5877162220649 \tabularnewline
17.8597386231158 \tabularnewline
4.57104866289501 \tabularnewline
-19.9806671545839 \tabularnewline
16.2210437593785 \tabularnewline
17.0939906922749 \tabularnewline
30.1343505324357 \tabularnewline
11.5907664565084 \tabularnewline
11.7612514894472 \tabularnewline
22.7551997743467 \tabularnewline
-17.580238997075 \tabularnewline
-6.03999798933819 \tabularnewline
-12.2570842732057 \tabularnewline
-9.22311072866705 \tabularnewline
-15.4943911196951 \tabularnewline
20.7994902083319 \tabularnewline
16.1910165667978 \tabularnewline
10.6925545206068 \tabularnewline
-0.508362965810193 \tabularnewline
-13.1265117907278 \tabularnewline
8.27511266420879 \tabularnewline
-30.2487049945539 \tabularnewline
-4.17717699887999 \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=300258&T=2

[TABLE]
[ROW][C]Estimated ARIMA Residuals[/C][/ROW]
[ROW][C]Value[/C][/ROW]
[ROW][C]-8.15513924605754[/C][/ROW]
[ROW][C]6.6880747370819[/C][/ROW]
[ROW][C]30.3742897379884[/C][/ROW]
[ROW][C]27.4024834450249[/C][/ROW]
[ROW][C]5.23270647013269[/C][/ROW]
[ROW][C]10.6950658059182[/C][/ROW]
[ROW][C]-19.3845551204331[/C][/ROW]
[ROW][C]34.083585584327[/C][/ROW]
[ROW][C]17.8153344133407[/C][/ROW]
[ROW][C]-2.08801002514429[/C][/ROW]
[ROW][C]-30.9230274545953[/C][/ROW]
[ROW][C]-11.9448080706406[/C][/ROW]
[ROW][C]3.35535603803601[/C][/ROW]
[ROW][C]-3.5197735358106[/C][/ROW]
[ROW][C]-12.2587168154232[/C][/ROW]
[ROW][C]-23.0257914520334[/C][/ROW]
[ROW][C]-12.7213614723632[/C][/ROW]
[ROW][C]-0.0446052607539968[/C][/ROW]
[ROW][C]-15.8935035121303[/C][/ROW]
[ROW][C]-30.0133113035481[/C][/ROW]
[ROW][C]-2.64949333691038[/C][/ROW]
[ROW][C]-12.6721192504347[/C][/ROW]
[ROW][C]8.86774823327596[/C][/ROW]
[ROW][C]3.31929351204326[/C][/ROW]
[ROW][C]-24.0335217807969[/C][/ROW]
[ROW][C]-2.81987022216345[/C][/ROW]
[ROW][C]-18.1629581890056[/C][/ROW]
[ROW][C]4.29604777202076[/C][/ROW]
[ROW][C]2.48296269181537[/C][/ROW]
[ROW][C]1.19634190483794[/C][/ROW]
[ROW][C]20.9917311367481[/C][/ROW]
[ROW][C]-11.3988511275893[/C][/ROW]
[ROW][C]16.7222053313835[/C][/ROW]
[ROW][C]4.61627418154512[/C][/ROW]
[ROW][C]10.2510768830507[/C][/ROW]
[ROW][C]5.98125858041203[/C][/ROW]
[ROW][C]-7.65703782555465[/C][/ROW]
[ROW][C]-14.9295832775051[/C][/ROW]
[ROW][C]4.03061921084373[/C][/ROW]
[ROW][C]-3.93162652161573[/C][/ROW]
[ROW][C]-16.616737696635[/C][/ROW]
[ROW][C]-8.15110360171093[/C][/ROW]
[ROW][C]28.3918415384869[/C][/ROW]
[ROW][C]14.0111632814351[/C][/ROW]
[ROW][C]-1.00222715300333[/C][/ROW]
[ROW][C]10.0437132119523[/C][/ROW]
[ROW][C]7.77621215996896[/C][/ROW]
[ROW][C]-14.0993071013754[/C][/ROW]
[ROW][C]19.1476224685539[/C][/ROW]
[ROW][C]0.643293957320566[/C][/ROW]
[ROW][C]2.77936012261853[/C][/ROW]
[ROW][C]-2.39225779963363[/C][/ROW]
[ROW][C]-5.25324600008298[/C][/ROW]
[ROW][C]12.2581851008354[/C][/ROW]
[ROW][C]11.9177249840377[/C][/ROW]
[ROW][C]10.5068162677944[/C][/ROW]
[ROW][C]-4.75682779044291[/C][/ROW]
[ROW][C]6.72114746146599[/C][/ROW]
[ROW][C]-3.42161933345778[/C][/ROW]
[ROW][C]-27.2289625585208[/C][/ROW]
[ROW][C]-0.859919505719517[/C][/ROW]
[ROW][C]-6.25231192010506[/C][/ROW]
[ROW][C]3.10937796290273[/C][/ROW]
[ROW][C]1.49368491101177[/C][/ROW]
[ROW][C]3.30093161643163[/C][/ROW]
[ROW][C]-6.17923825024445[/C][/ROW]
[ROW][C]-21.8764192059589[/C][/ROW]
[ROW][C]3.82013829760581[/C][/ROW]
[ROW][C]28.1815483184555[/C][/ROW]
[ROW][C]21.0700175513575[/C][/ROW]
[ROW][C]-8.08121925508476[/C][/ROW]
[ROW][C]-1.96749547034415[/C][/ROW]
[ROW][C]-14.5528731974646[/C][/ROW]
[ROW][C]-11.8462839345448[/C][/ROW]
[ROW][C]-14.3461058408639[/C][/ROW]
[ROW][C]-11.4887360613639[/C][/ROW]
[ROW][C]-12.1520508002723[/C][/ROW]
[ROW][C]-8.48323010597232[/C][/ROW]
[ROW][C]14.1286234902946[/C][/ROW]
[ROW][C]-16.5244786159565[/C][/ROW]
[ROW][C]6.10768292981265[/C][/ROW]
[ROW][C]12.5472797746834[/C][/ROW]
[ROW][C]9.01149570083362[/C][/ROW]
[ROW][C]-49.5284439444977[/C][/ROW]
[ROW][C]67.8526324077829[/C][/ROW]
[ROW][C]-0.834877985582352[/C][/ROW]
[ROW][C]-7.74949071339142[/C][/ROW]
[ROW][C]-15.8810126454209[/C][/ROW]
[ROW][C]-9.51791124314787[/C][/ROW]
[ROW][C]-2.4990775220067[/C][/ROW]
[ROW][C]-9.19082794705264[/C][/ROW]
[ROW][C]-8.16372485074317[/C][/ROW]
[ROW][C]-0.119646415903844[/C][/ROW]
[ROW][C]-49.5877162220649[/C][/ROW]
[ROW][C]17.8597386231158[/C][/ROW]
[ROW][C]4.57104866289501[/C][/ROW]
[ROW][C]-19.9806671545839[/C][/ROW]
[ROW][C]16.2210437593785[/C][/ROW]
[ROW][C]17.0939906922749[/C][/ROW]
[ROW][C]30.1343505324357[/C][/ROW]
[ROW][C]11.5907664565084[/C][/ROW]
[ROW][C]11.7612514894472[/C][/ROW]
[ROW][C]22.7551997743467[/C][/ROW]
[ROW][C]-17.580238997075[/C][/ROW]
[ROW][C]-6.03999798933819[/C][/ROW]
[ROW][C]-12.2570842732057[/C][/ROW]
[ROW][C]-9.22311072866705[/C][/ROW]
[ROW][C]-15.4943911196951[/C][/ROW]
[ROW][C]20.7994902083319[/C][/ROW]
[ROW][C]16.1910165667978[/C][/ROW]
[ROW][C]10.6925545206068[/C][/ROW]
[ROW][C]-0.508362965810193[/C][/ROW]
[ROW][C]-13.1265117907278[/C][/ROW]
[ROW][C]8.27511266420879[/C][/ROW]
[ROW][C]-30.2487049945539[/C][/ROW]
[ROW][C]-4.17717699887999[/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=300258&T=2

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=300258&T=2

As an alternative you can also use a QR Code:  
QR Code


The GUIDs for individual cells are displayed in the table below:

Estimated ARIMA Residuals
Value
-8.15513924605754
6.6880747370819
30.3742897379884
27.4024834450249
5.23270647013269
10.6950658059182
-19.3845551204331
34.083585584327
17.8153344133407
-2.08801002514429
-30.9230274545953
-11.9448080706406
3.35535603803601
-3.5197735358106
-12.2587168154232
-23.0257914520334
-12.7213614723632
-0.0446052607539968
-15.8935035121303
-30.0133113035481
-2.64949333691038
-12.6721192504347
8.86774823327596
3.31929351204326
-24.0335217807969
-2.81987022216345
-18.1629581890056
4.29604777202076
2.48296269181537
1.19634190483794
20.9917311367481
-11.3988511275893
16.7222053313835
4.61627418154512
10.2510768830507
5.98125858041203
-7.65703782555465
-14.9295832775051
4.03061921084373
-3.93162652161573
-16.616737696635
-8.15110360171093
28.3918415384869
14.0111632814351
-1.00222715300333
10.0437132119523
7.77621215996896
-14.0993071013754
19.1476224685539
0.643293957320566
2.77936012261853
-2.39225779963363
-5.25324600008298
12.2581851008354
11.9177249840377
10.5068162677944
-4.75682779044291
6.72114746146599
-3.42161933345778
-27.2289625585208
-0.859919505719517
-6.25231192010506
3.10937796290273
1.49368491101177
3.30093161643163
-6.17923825024445
-21.8764192059589
3.82013829760581
28.1815483184555
21.0700175513575
-8.08121925508476
-1.96749547034415
-14.5528731974646
-11.8462839345448
-14.3461058408639
-11.4887360613639
-12.1520508002723
-8.48323010597232
14.1286234902946
-16.5244786159565
6.10768292981265
12.5472797746834
9.01149570083362
-49.5284439444977
67.8526324077829
-0.834877985582352
-7.74949071339142
-15.8810126454209
-9.51791124314787
-2.4990775220067
-9.19082794705264
-8.16372485074317
-0.119646415903844
-49.5877162220649
17.8597386231158
4.57104866289501
-19.9806671545839
16.2210437593785
17.0939906922749
30.1343505324357
11.5907664565084
11.7612514894472
22.7551997743467
-17.580238997075
-6.03999798933819
-12.2570842732057
-9.22311072866705
-15.4943911196951
20.7994902083319
16.1910165667978
10.6925545206068
-0.508362965810193
-13.1265117907278
8.27511266420879
-30.2487049945539
-4.17717699887999


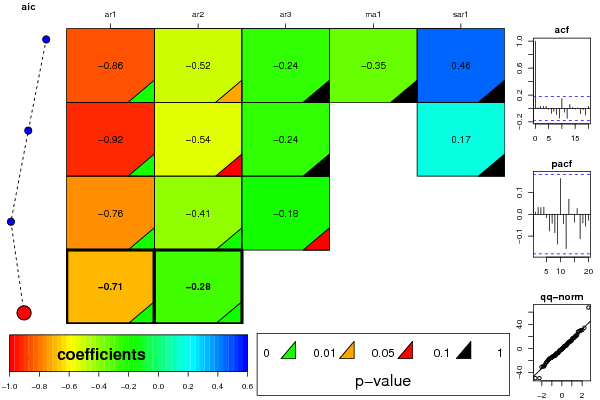
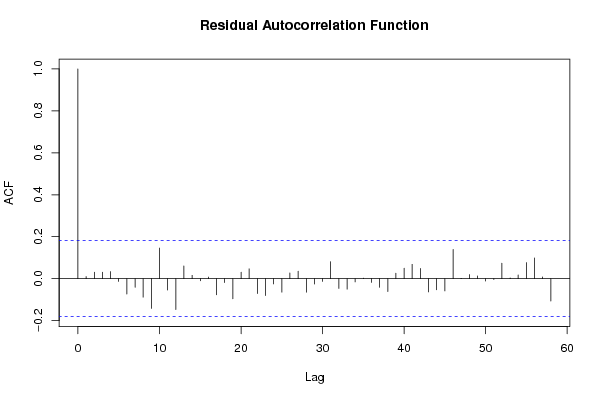
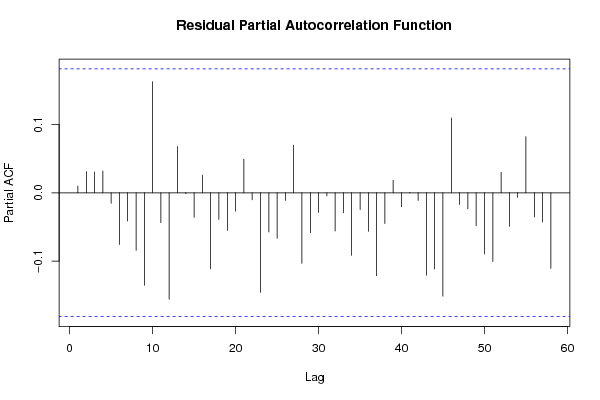
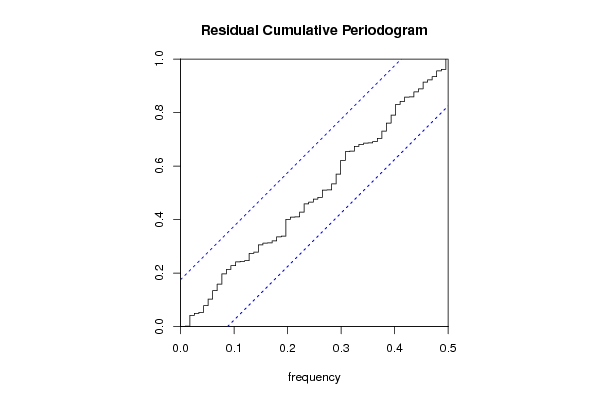
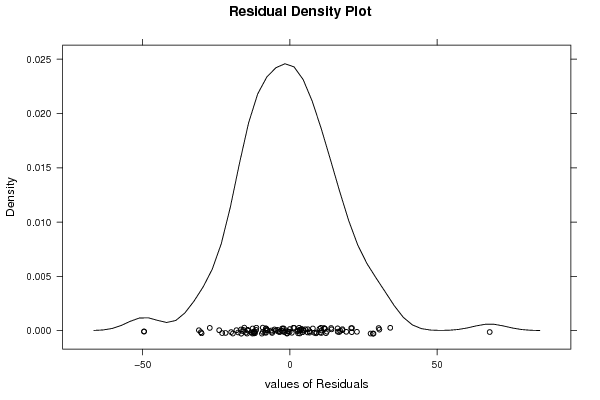
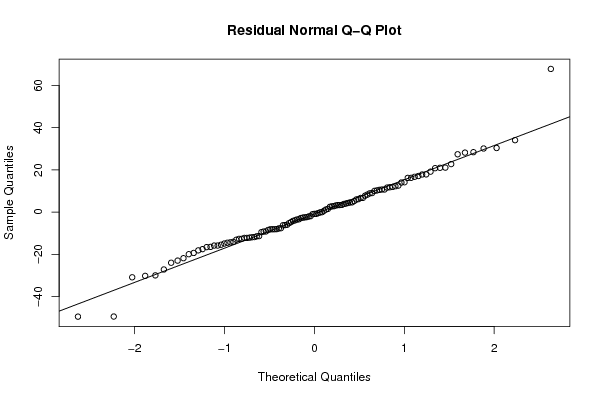
Figures (Output of Computation)

Input Parameters & R Code

Parameters (Session):
par1 = FALSE ; par2 = 1 ; par3 = 2 ; par4 = 0 ; par5 = 1 ; par6 = 3 ; par7 = 1 ; par8 = 2 ; par9 = 0 ;
Parameters (R input):
par1 = FALSE ; par2 = 1 ; par3 = 2 ; par4 = 0 ; par5 = 1 ; par6 = 3 ; par7 = 1 ; par8 = 1 ; par9 = 0 ;
R code (references can be found in the software module):
par9 <- '0'
par8 <- '2'
par7 <- '1'
par6 <- '3'
par5 <- '1'
par4 <- '0'
par3 <- '2'
par2 <- '1'
par1 <- 'FALSE'
library(lattice)
if (par1 == 'TRUE') par1 <- TRUE
if (par1 == 'FALSE') par1 <- FALSE
par2 <- as.numeric(par2) #Box-Cox lambda transformation parameter
par3 <- as.numeric(par3) #degree of non-seasonal differencing
par4 <- as.numeric(par4) #degree of seasonal differencing
par5 <- as.numeric(par5) #seasonal period
par6 <- as.numeric(par6) #degree (p) of the non-seasonal AR(p) polynomial
par7 <- as.numeric(par7) #degree (q) of the non-seasonal MA(q) polynomial
par8 <- as.numeric(par8) #degree (P) of the seasonal AR(P) polynomial
par9 <- as.numeric(par9) #degree (Q) of the seasonal MA(Q) polynomial
armaGR <- function(arima.out, names, n){
try1 <- arima.out$coef
try2 <- sqrt(diag(arima.out$var.coef))
try.data.frame  <- data.frame(matrix(NA,ncol=4,nrow=length(names)))
dimnames(try.data.frame) <- list(names,c('coef','std','tstat','pv'))
try.data.frame[,1] <- try1
for(i in 1:length(try2)) try.data.frame[which(rownames(try.data.frame)==names(try2)[i]),2] <- try2[i]
try.data.frame[,3] <- try.data.frame[,1] / try.data.frame[,2]
try.data.frame[,4] <- round((1-pt(abs(try.data.frame[,3]),df=n-(length(try2)+1)))*2,5)
vector <- rep(NA,length(names))
vector[is.na(try.data.frame[,4])] <- 0
maxi <- which.max(try.data.frame[,4])
continue <- max(try.data.frame[,4],na.rm=TRUE) > .05
vector[maxi] <- 0
list(summary=try.data.frame,next.vector=vector,continue=continue)
}
arimaSelect <- function(series, order=c(13,0,0), seasonal=list(order=c(2,0,0),period=12), include.mean=F){
nrc <- order[1]+order[3]+seasonal$order[1]+seasonal$order[3]
coeff <- matrix(NA, nrow=nrc*2, ncol=nrc)
pval <- matrix(NA, nrow=nrc*2, ncol=nrc)
mylist <- rep(list(NULL), nrc)
names  <- NULL
if(order[1] > 0) names <- paste('ar',1:order[1],sep='')
if(order[3] > 0) names <- c( names , paste('ma',1:order[3],sep='') )
if(seasonal$order[1] > 0) names <- c(names, paste('sar',1:seasonal$order[1],sep=''))
if(seasonal$order[3] > 0) names <- c(names, paste('sma',1:seasonal$order[3],sep=''))
arima.out <- arima(series, order=order, seasonal=seasonal, include.mean=include.mean, method='ML')
mylist[[1]] <- arima.out
last.arma <- armaGR(arima.out, names, length(series))
mystop <- FALSE
i <- 1
coeff[i,] <- last.arma[[1]][,1]
pval [i,] <- last.arma[[1]][,4]
i <- 2
aic <- arima.out$aic
while(!mystop){
mylist[[i]] <- arima.out
arima.out <- arima(series, order=order, seasonal=seasonal, include.mean=include.mean, method='ML', fixed=last.arma$next.vector)
aic <- c(aic, arima.out$aic)
last.arma <- armaGR(arima.out, names, length(series))
mystop <- !last.arma$continue
coeff[i,] <- last.arma[[1]][,1]
pval [i,] <- last.arma[[1]][,4]
i <- i+1
}
list(coeff, pval, mylist, aic=aic)
}
arimaSelectplot <- function(arimaSelect.out,noms,choix){
noms <- names(arimaSelect.out[[3]][[1]]$coef)
coeff <- arimaSelect.out[[1]]
k <- min(which(is.na(coeff[,1])))-1
coeff <- coeff[1:k,]
pval  <- arimaSelect.out[[2]][1:k,]
aic   <- arimaSelect.out$aic[1:k]
coeff[coeff==0] <- NA
n <- ncol(coeff)
if(missing(choix)) choix <- k
layout(matrix(c(1,1,1,2,
3,3,3,2,
3,3,3,4,
5,6,7,7),nr=4),
widths=c(10,35,45,15),
heights=c(30,30,15,15))
couleurs <- rainbow(75)[1:50]#(50)
ticks <- pretty(coeff)
par(mar=c(1,1,3,1))
plot(aic,k:1-.5,type='o',pch=21,bg='blue',cex=2,axes=F,lty=2,xpd=NA)
points(aic[choix],k-choix+.5,pch=21,cex=4,bg=2,xpd=NA)
title('aic',line=2)
par(mar=c(3,0,0,0))
plot(0,axes=F,xlab='',ylab='',xlim=range(ticks),ylim=c(.1,1))
rect(xleft  = min(ticks) + (0:49)/50*(max(ticks)-min(ticks)),
xright = min(ticks) + (1:50)/50*(max(ticks)-min(ticks)),
ytop   = rep(1,50),
ybottom= rep(0,50),col=couleurs,border=NA)
axis(1,ticks)
rect(xleft=min(ticks),xright=max(ticks),ytop=1,ybottom=0)
text(mean(coeff,na.rm=T),.5,'coefficients',cex=2,font=2)
par(mar=c(1,1,3,1))
image(1:n,1:k,t(coeff[k:1,]),axes=F,col=couleurs,zlim=range(ticks))
for(i in 1:n) for(j in 1:k) if(!is.na(coeff[j,i])) {
if(pval[j,i]<.01)                            symb = 'green'
else if( (pval[j,i]<.05) & (pval[j,i]>=.01)) symb = 'orange'
else if( (pval[j,i]<.1)  & (pval[j,i]>=.05)) symb = 'red'
else                                         symb = 'black'
polygon(c(i+.5   ,i+.2   ,i+.5   ,i+.5),
c(k-j+0.5,k-j+0.5,k-j+0.8,k-j+0.5),
col=symb)
if(j==choix)  {
rect(xleft=i-.5,
xright=i+.5,
ybottom=k-j+1.5,
ytop=k-j+.5,
lwd=4)
text(i,
k-j+1,
round(coeff[j,i],2),
cex=1.2,
font=2)
}
else{
rect(xleft=i-.5,xright=i+.5,ybottom=k-j+1.5,ytop=k-j+.5)
text(i,k-j+1,round(coeff[j,i],2),cex=1.2,font=1)
}
}
axis(3,1:n,noms)
par(mar=c(0.5,0,0,0.5))
plot(0,axes=F,xlab='',ylab='',type='n',xlim=c(0,8),ylim=c(-.2,.8))
cols <- c('green','orange','red','black')
niv  <- c('0','0.01','0.05','0.1')
for(i in 0:3){
polygon(c(1+2*i   ,1+2*i   ,1+2*i-.5   ,1+2*i),
c(.4      ,.7      , .4        , .4),
col=cols[i+1])
text(2*i,0.5,niv[i+1],cex=1.5)
}
text(8,.5,1,cex=1.5)
text(4,0,'p-value',cex=2)
box()
residus <- arimaSelect.out[[3]][[choix]]$res
par(mar=c(1,2,4,1))
acf(residus,main='')
title('acf',line=.5)
par(mar=c(1,2,4,1))
pacf(residus,main='')
title('pacf',line=.5)
par(mar=c(2,2,4,1))
qqnorm(residus,main='')
title('qq-norm',line=.5)
qqline(residus)
residus
}
if (par2 == 0) x <- log(x)
if (par2 != 0) x <- x^par2
(selection <- arimaSelect(x, order=c(par6,par3,par7), seasonal=list(order=c(par8,par4,par9), period=par5)))
bitmap(file='test1.png')
resid <- arimaSelectplot(selection)
dev.off()
resid
bitmap(file='test2.png')
acf(resid,length(resid)/2, main='Residual Autocorrelation Function')
dev.off()
bitmap(file='test3.png')
pacf(resid,length(resid)/2, main='Residual Partial Autocorrelation Function')
dev.off()
bitmap(file='test4.png')
cpgram(resid, main='Residual Cumulative Periodogram')
dev.off()
bitmap(file='test5.png')
hist(resid, main='Residual Histogram', xlab='values of Residuals')
dev.off()
bitmap(file='test6.png')
densityplot(~resid,col='black',main='Residual Density Plot', xlab='values of Residuals')
dev.off()
bitmap(file='test7.png')
qqnorm(resid, main='Residual Normal Q-Q Plot')
qqline(resid)
dev.off()
ncols <- length(selection[[1]][1,])
nrows <- length(selection[[2]][,1])-1
load(file='createtable')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,'ARIMA Parameter Estimation and Backward Selection', ncols+1,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'Iteration', header=TRUE)
for (i in 1:ncols) {
a<-table.element(a,names(selection[[3]][[1]]$coef)[i],header=TRUE)
}
a<-table.row.end(a)
for (j in 1:nrows) {
a<-table.row.start(a)
mydum <- 'Estimates ('
mydum <- paste(mydum,j)
mydum <- paste(mydum,')')
a<-table.element(a,mydum, header=TRUE)
for (i in 1:ncols) {
a<-table.element(a,round(selection[[1]][j,i],4))
}
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'(p-val)', header=TRUE)
for (i in 1:ncols) {
mydum <- '('
mydum <- paste(mydum,round(selection[[2]][j,i],4),sep='')
mydum <- paste(mydum,')')
a<-table.element(a,mydum)
}
a<-table.row.end(a)
}
a<-table.end(a)
table.save(a,file='mytable.tab')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,'Estimated ARIMA Residuals', 1,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a,'Value', 1,TRUE)
a<-table.row.end(a)
for (i in (par4*par5+par3):length(resid)) {
a<-table.row.start(a)
a<-table.element(a,resid[i])
a<-table.row.end(a)
}
a<-table.end(a)
table.save(a,file='mytable1.tab')