| Multiple Linear Regression - Estimated Regression Equation |
| IndustriŽle_productie[t] = + 103.9375 + 6.78630952380952x[t] + e[t] |
| Multiple Linear Regression - Ordinary Least Squares | |||||
| Variable | Parameter | S.D. | T-STAT H0: parameter = 0 | 2-tail p-value | 1-tail p-value |
| (Intercept) | 103.9375 | 1.06455 | 97.6351 | 0 | 0 |
| x | 6.78630952380952 | 1.814352 | 3.7403 | 0.000418 | 0.000209 |
| Multiple Linear Regression - Regression Statistics | |
| Multiple R | 0.43780409846228 |
| R-squared | 0.19167242863037 |
| Adjusted R-squared | 0.177971961319020 |
| F-TEST (value) | 13.9902110106555 |
| F-TEST (DF numerator) | 1 |
| F-TEST (DF denominator) | 59 |
| p-value | 0.000417895249223532 |
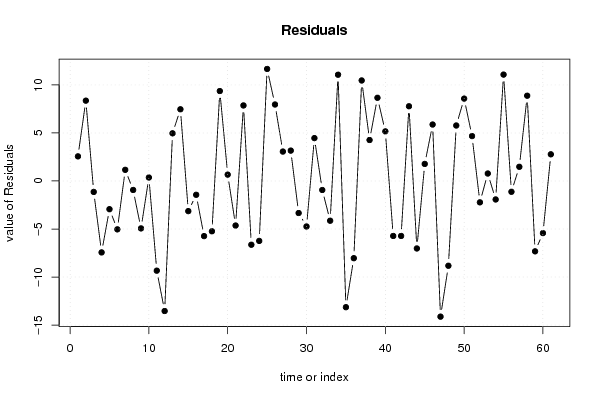
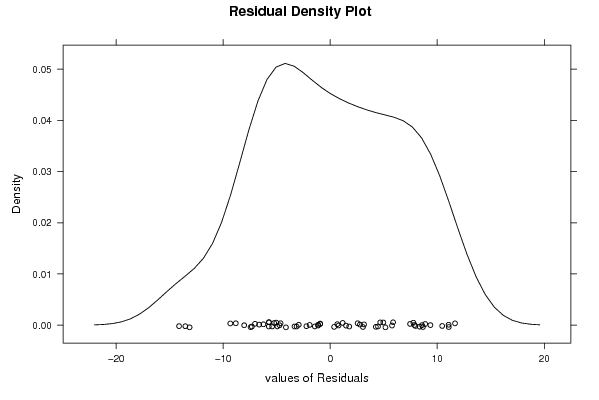
| Multiple Linear Regression - Residual Statistics | |
| Residual Standard Deviation | 6.73280842155216 |
| Sum Squared Residuals | 2674.51184523810 |
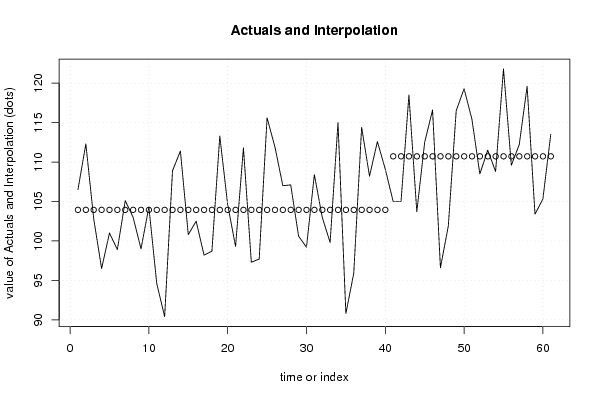
| Multiple Linear Regression - Actuals, Interpolation, and Residuals | |||
| Time or Index | Actuals | Interpolation Forecast | Residuals Prediction Error |
| 1 | 106.5 | 103.9375 | 2.56250000000008 |
| 2 | 112.3 | 103.9375 | 8.3625 |
| 3 | 102.8 | 103.9375 | -1.13750000000000 |
| 4 | 96.5 | 103.9375 | -7.4375 |
| 5 | 101 | 103.9375 | -2.9375 |
| 6 | 98.9 | 103.9375 | -5.0375 |
| 7 | 105.1 | 103.9375 | 1.16249999999999 |
| 8 | 103 | 103.9375 | -0.937500000000001 |
| 9 | 99 | 103.9375 | -4.9375 |
| 10 | 104.3 | 103.9375 | 0.362499999999996 |
| 11 | 94.6 | 103.9375 | -9.3375 |
| 12 | 90.4 | 103.9375 | -13.5375 |
| 13 | 108.9 | 103.9375 | 4.9625 |
| 14 | 111.4 | 103.9375 | 7.4625 |
| 15 | 100.8 | 103.9375 | -3.13750000000000 |
| 16 | 102.5 | 103.9375 | -1.43750000000000 |
| 17 | 98.2 | 103.9375 | -5.7375 |
| 18 | 98.7 | 103.9375 | -5.2375 |
| 19 | 113.3 | 103.9375 | 9.3625 |
| 20 | 104.6 | 103.9375 | 0.662499999999993 |
| 21 | 99.3 | 103.9375 | -4.6375 |
| 22 | 111.8 | 103.9375 | 7.8625 |
| 23 | 97.3 | 103.9375 | -6.6375 |
| 24 | 97.7 | 103.9375 | -6.2375 |
| 25 | 115.6 | 103.9375 | 11.6625 |
| 26 | 111.9 | 103.9375 | 7.9625 |
| 27 | 107 | 103.9375 | 3.0625 |
| 28 | 107.1 | 103.9375 | 3.16249999999999 |
| 29 | 100.6 | 103.9375 | -3.33750000000001 |
| 30 | 99.2 | 103.9375 | -4.7375 |
| 31 | 108.4 | 103.9375 | 4.4625 |
| 32 | 103 | 103.9375 | -0.937500000000001 |
| 33 | 99.8 | 103.9375 | -4.13750000000000 |
| 34 | 115 | 103.9375 | 11.0625 |
| 35 | 90.8 | 103.9375 | -13.1375 |
| 36 | 95.9 | 103.9375 | -8.0375 |
| 37 | 114.4 | 103.9375 | 10.4625 |
| 38 | 108.2 | 103.9375 | 4.2625 |
| 39 | 112.6 | 103.9375 | 8.6625 |
| 40 | 109.1 | 103.9375 | 5.16249999999999 |
| 41 | 105 | 110.723809523810 | -5.72380952380952 |
| 42 | 105 | 110.723809523810 | -5.72380952380952 |
| 43 | 118.5 | 110.723809523810 | 7.77619047619048 |
| 44 | 103.7 | 110.723809523810 | -7.02380952380952 |
| 45 | 112.5 | 110.723809523810 | 1.77619047619048 |
| 46 | 116.6 | 110.723809523810 | 5.87619047619047 |
| 47 | 96.6 | 110.723809523810 | -14.1238095238095 |
| 48 | 101.9 | 110.723809523810 | -8.82380952380952 |
| 49 | 116.5 | 110.723809523810 | 5.77619047619048 |
| 50 | 119.3 | 110.723809523810 | 8.57619047619047 |
| 51 | 115.4 | 110.723809523810 | 4.67619047619048 |
| 52 | 108.5 | 110.723809523810 | -2.22380952380952 |
| 53 | 111.5 | 110.723809523810 | 0.776190476190478 |
| 54 | 108.8 | 110.723809523810 | -1.92380952380952 |
| 55 | 121.8 | 110.723809523810 | 11.0761904761905 |
| 56 | 109.6 | 110.723809523810 | -1.12380952380953 |
| 57 | 112.2 | 110.723809523810 | 1.47619047619048 |
| 58 | 119.6 | 110.723809523810 | 8.87619047619047 |
| 59 | 103.4 | 110.723809523810 | -7.32380952380952 |
| 60 | 105.3 | 110.723809523810 | -5.42380952380953 |
| 61 | 113.5 | 110.723809523810 | 2.77619047619048 |