FreeStatistics.org

Free Statistics

of Irreproducible Research!

Description of Statistical Computation

Author's title

Author*The author of this computation has been verified*
R Software Modulerwasp_Simple Regression Y ~ X.wasp
Title produced by softwareSimple Linear Regression
Date of computationWed, 14 Dec 2016 18:17:07 +0100
Cite this page as followsStatistical Computations at FreeStatistics.org, Office for Research Development and Education, URL https://freestatistics.org/blog/index.php?v=date/2016/Dec/14/t1481738720gjuh7hyhyia6pm7.htm/, Retrieved Fri, 01 Nov 2024 04:48:41 +0100
Statistical Computations at FreeStatistics.org, Office for Research Development and Education, URL https://freestatistics.org/blog/index.php?pk=, Retrieved Fri, 01 Nov 2024 04:48:41 +0100
QR Codes:

Original text written by user:
IsPrivate?No (this computation is public)
User-defined keywords
Estimated Impact0

Tree of Dependent Computations

Dataset

Dataseries X:
Download CSV
Histogram
Boxplots 
3	4	3	4	18
5	5	5	4	19
5	4	4	4	18
5	4	4	4	15
4	4	3	4	19
5	5	5	5	19
5	4	3	3	19
5	5	4	1	18
5	4	3	3	20
5	5	5	4	14
5	5	5	5	18
5	5	4	4	19
4	4	3	4	16
3	4	4	3	18
5	5	5	5	18
5	4	3	4	17
5	3	3	5	19
4	4	4	4	19
2	5	1	2	17
5	5	4	5	18
5	5	4	5	16
5	5	4	2	20
4	4	4	3	13
4	5	5	4	19
4	5	4	4	15
5	5	4	5	17
5	5	4	3	17
5	5	4	5	17
5	5	5	5	19
1	1	1	2	18
5	5	4	5	19
4	5	4	3	20
4	4	4	3	16
4	4	4	4	17
5	5	4	4	16
4	4	5	3	16
4	4	4	3	16
5	4	4	4	16
5	5	5	5	17
5	5	5	4	18
2	2	1	2	16
3	3	3	4	16
4	5	3	4	16
5	5	4	4	19
5	5	5	3	16
4	4	4	4	17
5	5	3	4	19
5	5	5	4	17
4	4	4	4	17
5	5	4	5	15
4	5	3	1	16
4	4	4	4	16
3	4	3	3	16
4	4	3	1	17
4	5	4	4	18
5	4	4	4	18
4	5	4	4	18
4	5	4	3	19
4	4	4	4	14
4	3	3	4	13
4	4	4	4	18
2	4	4	3	16
4	5	4	3	15
4	4	3	3	18
5	5	5	5	18
3	3	3	3	16
3	4	3	3	19
5	4	5	4	17
4	3	3	4	17
5	5	5	4	19
4	5	4	5	19
4	3	3	4	20
5	5	3	5	19
5	5	5	4	18
5	4	3	3	16
4	4	3	3	16
5	4	4	4	15
5	5	5	4	20
2	5	4	2	16
5	4	5	5	16
5	5	4	4	20
5	5	5	5	20
5	4	4	2	18
4	4	4	3	15
4	4	4	3	14
5	5	5	5	16
4	4	4	3	14
5	5	5	4	18
5	5	4	4	20
5	4	5	4	20
4	4	4	3	18
5	5	5	5	20
5	5	5	2	14
3	4	2	3	20
5	4	5	4	17
5	5	5	4	20
5	5	5	5	14
4	4	5	4	20
4	4	4	3	19
4	4	4	4	18
5	5	5	3	17
5	5	4	4	17
4	4	2	4	19
3	4	4	4	15
3	4	3	2	18
4	4	5	4	15
4	4	3	3	16
5	5	4	4	16
5	4	4	4	20
4	4	5	4	18
5	5	5	5	20
5	4	4	3	18
4	4	3	3	17
4	4	3	4	19
5	5	4	4	18
5	5	5	5	19
5	5	3	4	17
5	5	3	4	18
4	5	4	4	17
5	4	4	4	16
3	4	4	4	19
5	5	4	3	18
5	4	5	4	17
4	5	4	4	18
5	5	5	5	16
4	4	4	3	20
4	4	4	4	14
4	4	4	3	17
4	4	5	5	13
2	3	2	4	13
4	4	4	3	17
5	4	5	4	18
5	5	5	5	16
4	4	4	2	19
5	4	4	2	17
5	4	4	4	16
5	4	5	4	17
5	5	5	5	17
5	3	5	4	17
5	4	5	4	20
4	4	4	3	14
5	4	4	3	20
3	3	3	2	19
3	4	4	4	16
4	5	4	5	19
4	5	4	4	17
3	5	3	5	19
3	4	3	2	20
5	5	5	4	19
5	5	4	4	19
5	4	4	2	16
5	4	4	4	18
5	5	5	4	16
5	4	5	4	17
5	5	5	4	18
5	4	5	2	16
4	4	4	4	17
4	4	5	3	15
2	4	5	3	18

Tables (Output of Computation)





Summary of computational transaction
Raw Input view raw input (R code)
Raw Outputview raw output of R engine
Computing time7 seconds
R ServerBig Analytics Cloud Computing Center

\begin{tabular}{lllllllll}
\hline
Summary of computational transaction \tabularnewline
Raw Input view raw input (R code)  \tabularnewline
Raw Outputview raw output of R engine  \tabularnewline
Computing time7 seconds \tabularnewline
R ServerBig Analytics Cloud Computing Center \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=&T=0

[TABLE]
[ROW]
Summary of computational transaction[/C][/ROW] [ROW]Raw Input[/C] view raw input (R code) [/C][/ROW] [ROW]Raw Output[/C]view raw output of R engine [/C][/ROW] [ROW]Computing time[/C]7 seconds[/C][/ROW] [ROW]R Server[/C]Big Analytics Cloud Computing Center[/C][/ROW] [/TABLE] Source: https://freestatistics.org/blog/index.php?pk=&T=0

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=&T=0

As an alternative you can also use a QR Code:  
QR Code


The GUIDs for individual cells are displayed in the table below:

Summary of computational transaction
Raw Input view raw input (R code)
Raw Outputview raw output of R engine
Computing time7 seconds
R ServerBig Analytics Cloud Computing Center






Linear Regression Model
Y ~ X
coefficients:
EstimateStd. Errort valuePr(>|t|)
(Intercept)1.6310.3784.3130
X0.6220.0867.2480
- - -
Residual Std. Err. 0.73 on 157 df
Multiple R-sq. 0.251
95% CI Multiple R-sq. [0.103, 0.48]
Adjusted R-sq. 0.246

\begin{tabular}{lllllllll}
\hline
Linear Regression Model \tabularnewline
Y ~ X \tabularnewline
coefficients: &   \tabularnewline
  & Estimate & Std. Error & t value & Pr(>|t|) \tabularnewline
(Intercept) & 1.631 & 0.378 & 4.313 & 0 \tabularnewline
X & 0.622 & 0.086 & 7.248 & 0 \tabularnewline
- - -  &   \tabularnewline
Residual Std. Err.  & 0.73  on  157 df \tabularnewline
Multiple R-sq.  & 0.251 \tabularnewline
95% CI Multiple R-sq.  & [0.103, 0.48] \tabularnewline
Adjusted R-sq.  & 0.246 \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=&T=1

[TABLE]
[ROW][C]Linear Regression Model[/C][/ROW]
[ROW][C]Y ~ X[/C][/ROW]
[ROW][C]coefficients:[/C][C] [/C][/ROW]
[ROW][C] [/C][C]Estimate[/C][C]Std. Error[/C][C]t value[/C][C]Pr(>|t|)[/C][/ROW]
[C](Intercept)[/C][C]1.631[/C][C]0.378[/C][C]4.313[/C][C]0[/C][/ROW]
[C]X[/C][C]0.622[/C][C]0.086[/C][C]7.248[/C][C]0[/C][/ROW]
[ROW][C]- - - [/C][C] [/C][/ROW]
[ROW][C]Residual Std. Err. [/C][C]0.73  on  157 df[/C][/ROW]
[ROW][C]Multiple R-sq. [/C][C]0.251[/C][/ROW]
[ROW][C]95% CI Multiple R-sq. [/C][C][0.103, 0.48][/C][/ROW]
[ROW][C]Adjusted R-sq. [/C][C]0.246[/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=&T=1

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=&T=1

As an alternative you can also use a QR Code:  
QR Code


The GUIDs for individual cells are displayed in the table below:

Linear Regression Model
Y ~ X
coefficients:
EstimateStd. Errort valuePr(>|t|)
(Intercept)1.6310.3784.3130
X0.6220.0867.2480
- - -
Residual Std. Err. 0.73 on 157 df
Multiple R-sq. 0.251
95% CI Multiple R-sq. [0.103, 0.48]
Adjusted R-sq. 0.246






ANOVA Statistics
DfSum SqMean SqF valuePr(>F)
ITH2127.99427.99452.530
Residuals15783.6670.533 

\begin{tabular}{lllllllll}
\hline
ANOVA Statistics \tabularnewline
  & Df & Sum Sq & Mean Sq & F value & Pr(>F) \tabularnewline
ITH2 & 1 & 27.994 & 27.994 & 52.53 & 0 \tabularnewline
Residuals & 157 & 83.667 & 0.533 &   &   \tabularnewline
\hline
\end{tabular}
%Source: https://freestatistics.org/blog/index.php?pk=&T=2

[TABLE]
[ROW][C]ANOVA Statistics[/C][/ROW]
[ROW][C] [/C][C]Df[/C][C]Sum Sq[/C][C]Mean Sq[/C][C]F value[/C][C]Pr(>F)[/C][/ROW]
[ROW][C]ITH2[/C][C]1[/C][C]27.994[/C][C]27.994[/C][C]52.53[/C][C]0[/C][/ROW]
[ROW][C]Residuals[/C][C]157[/C][C]83.667[/C][C]0.533[/C][C] [/C][C] [/C][/ROW]
[/TABLE]
Source: https://freestatistics.org/blog/index.php?pk=&T=2

Globally Unique Identifier (entire table): ba.freestatistics.org/blog/index.php?pk=&T=2

As an alternative you can also use a QR Code:  
QR Code


The GUIDs for individual cells are displayed in the table below:

ANOVA Statistics
DfSum SqMean SqF valuePr(>F)
ITH2127.99427.99452.530
Residuals15783.6670.533


Figures (Output of Computation)

Input Parameters & R Code

Parameters (Session):
par1 = 1122215555551 ; par2 = 22111Do not include Seasonal DummiesDo not include Seasonal DummiesDo not include Seasonal DummiesDo not include Seasonal DummiesDo not include Seasonal DummiesDo not include Seasonal DummiesDo not include Seasonal DummiesDo not include Seasonal DummiesDo not include Seasonal Dummies2 ; par3 = TRUETRUETRUENo Linear TrendTRUENo Linear TrendNo Linear TrendNo Linear TrendNo Linear TrendNo Linear TrendNo Linear TrendNo Linear TrendNo Linear TrendNo Linear TrendTRUE ; par4 = 555000000 ; par5 = 000000000 ;
Parameters (R input):
par1 = 1 ; par2 = 2 ; par3 = TRUE ;
R code (references can be found in the software module):
library(boot)
cat1 <- as.numeric(par1)
cat2<- as.numeric(par2)
intercept<-as.logical(par3)
x <- na.omit(t(x))
rsq <- function(formula, data, indices) {
d <- data[indices,] # allows boot to select sample
fit <- lm(formula, data=d)
return(summary(fit)$r.square)
}
xdf<-data.frame(na.omit(t(y)))
(V1<-dimnames(y)[[1]][cat1])
(V2<-dimnames(y)[[1]][cat2])
xdf <- data.frame(xdf[[cat1]], xdf[[cat2]])
names(xdf)<-c('Y', 'X')
if(intercept == FALSE) (lmxdf<-lm(Y~ X - 1, data = xdf) ) else (lmxdf<-lm(Y~ X, data = xdf) )
(results <- boot(data=xdf, statistic=rsq, R=1000, formula=Y~X))
sumlmxdf<-summary(lmxdf)
(aov.xdf<-aov(lmxdf) )
(anova.xdf<-anova(lmxdf) )
load(file='createtable')
a<-table.start()
nc <- ncol(sumlmxdf$'coefficients')
nr <- nrow(sumlmxdf$'coefficients')
a<-table.row.start(a)
a<-table.element(a,'Linear Regression Model', nc+1,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, lmxdf$call['formula'],nc+1)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'coefficients:',1,TRUE)
a<-table.element(a, ' ',nc,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, ' ',1,TRUE)
for(i in 1 : nc){
a<-table.element(a, dimnames(sumlmxdf$'coefficients')[[2]][i],1,TRUE)
}#end header
a<-table.row.end(a)
for(i in 1: nr){
a<-table.element(a,dimnames(sumlmxdf$'coefficients')[[1]][i] ,1,TRUE)
for(j in 1 : nc){
a<-table.element(a, round(sumlmxdf$coefficients[i, j], digits=3), 1 ,FALSE)
}
a<-table.row.end(a)
}
a<-table.row.start(a)
a<-table.element(a, '- - - ',1,TRUE)
a<-table.element(a, ' ',nc,FALSE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'Residual Std. Err. ',1,TRUE)
a<-table.element(a, paste(round(sumlmxdf$'sigma', digits=3), ' on ', sumlmxdf$'df'[2], 'df') ,nc, FALSE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'Multiple R-sq. ',1,TRUE)
a<-table.element(a, round(sumlmxdf$'r.squared', digits=3) ,nc, FALSE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, '95% CI Multiple R-sq. ',1,TRUE)
a<-table.element(a, paste('[',round(boot.ci(results,type='bca')$bca[1,4], digits=3),', ', round(boot.ci(results,type='bca')$bca[1,5], digits=3), ']',sep='') ,nc, FALSE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'Adjusted R-sq. ',1,TRUE)
a<-table.element(a, round(sumlmxdf$'adj.r.squared', digits=3) ,nc, FALSE)
a<-table.row.end(a)
a<-table.end(a)
table.save(a,file='mytable.tab')
a<-table.start()
a<-table.row.start(a)
a<-table.element(a,'ANOVA Statistics', 5+1,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, ' ',1,TRUE)
a<-table.element(a, 'Df',1,TRUE)
a<-table.element(a, 'Sum Sq',1,TRUE)
a<-table.element(a, 'Mean Sq',1,TRUE)
a<-table.element(a, 'F value',1,TRUE)
a<-table.element(a, 'Pr(>F)',1,TRUE)
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, V2,1,TRUE)
a<-table.element(a, anova.xdf$Df[1])
a<-table.element(a, round(anova.xdf$'Sum Sq'[1], digits=3))
a<-table.element(a, round(anova.xdf$'Mean Sq'[1], digits=3))
a<-table.element(a, round(anova.xdf$'F value'[1], digits=3))
a<-table.element(a, round(anova.xdf$'Pr(>F)'[1], digits=3))
a<-table.row.end(a)
a<-table.row.start(a)
a<-table.element(a, 'Residuals',1,TRUE)
a<-table.element(a, anova.xdf$Df[2])
a<-table.element(a, round(anova.xdf$'Sum Sq'[2], digits=3))
a<-table.element(a, round(anova.xdf$'Mean Sq'[2], digits=3))
a<-table.element(a, ' ')
a<-table.element(a, ' ')
a<-table.row.end(a)
a<-table.end(a)
table.save(a,file='mytable1.tab')
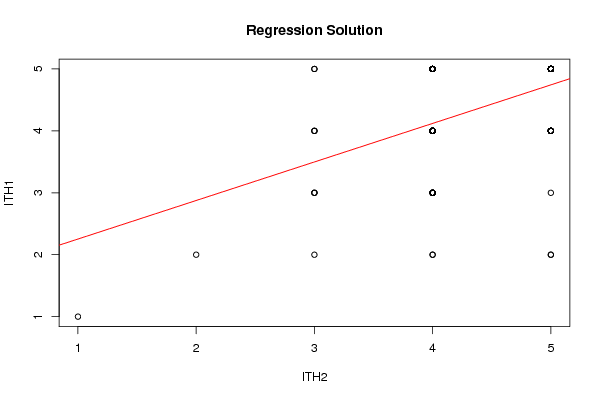
bitmap(file='regressionplot.png')
plot(Y~ X, data=xdf, xlab=V2, ylab=V1, main='Regression Solution')
if(intercept == TRUE) abline(coef(lmxdf), col='red')
if(intercept == FALSE) abline(0.0, coef(lmxdf), col='red')
dev.off()
library(car)
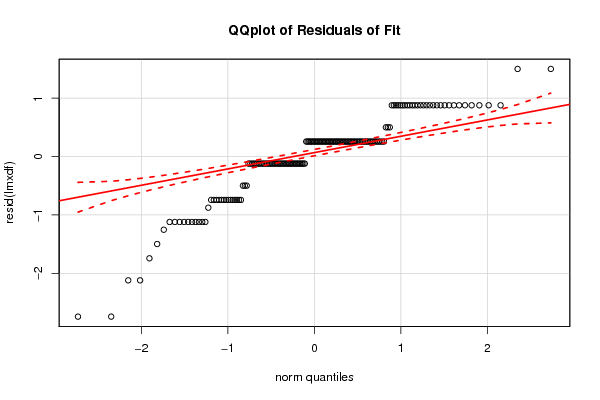
bitmap(file='residualsQQplot.png')
qqPlot(resid(lmxdf), main='QQplot of Residuals of Fit')
dev.off()
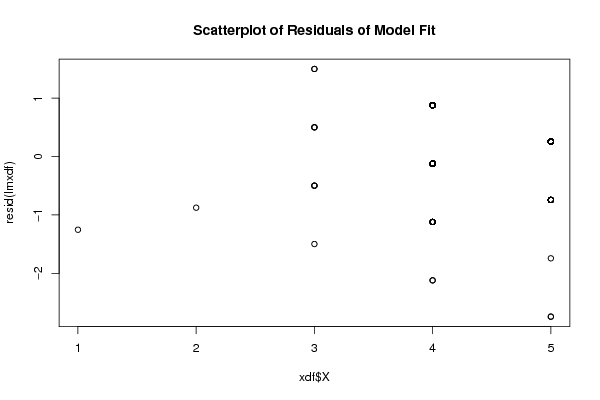
bitmap(file='residualsplot.png')
plot(xdf$X, resid(lmxdf), main='Scatterplot of Residuals of Model Fit')
dev.off()
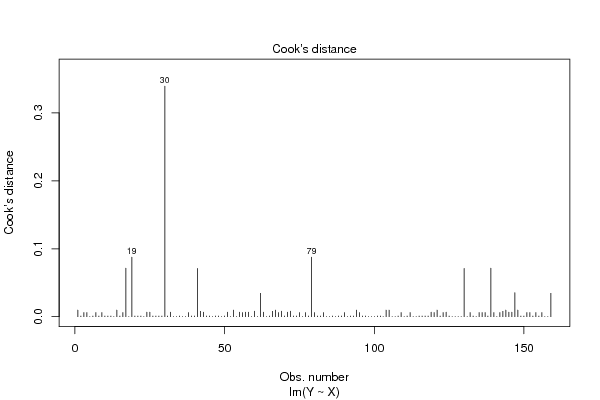
bitmap(file='cooksDistanceLmplot.png')
plot(lmxdf, which=4)
dev.off()